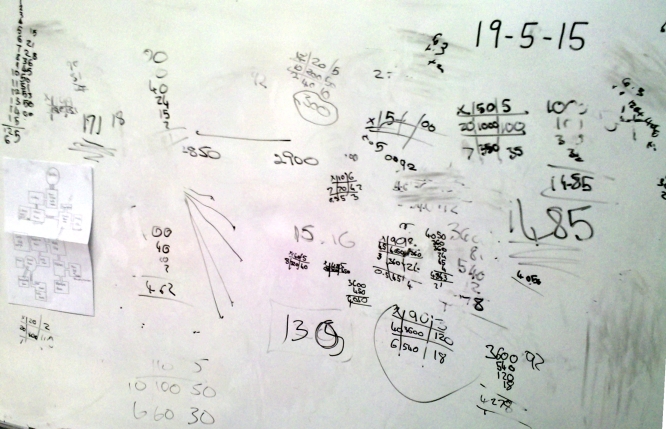A Conversation with Kitty
Of course, one of the great features offered by even the simplest programming and coding activities is that when a procedure doesn’t do what it should children respond positively, and see initial failure as a stimulus to find out what went wrong and do better next time.
But I’ve never known a child express this as strongly as Kitty. She believes so strongly in this problem-solving aspect that she actually wants her programs to fail, because if a program works immediately she misses out on what she really enjoys, which is figuring out what went wrong and how to correct it.
Which raises the obvious question – how do I devise mathematical activities that children want to fail at in such a positive way?
.
.
Farewell Amy
I’d be grateful if you’d help me in a little experiment.
In the photo the letters A to J stand, in some order, for the digits 0 to 9. (As you’ll no doubt guess, a two-letter item stands for a number such as 23 rather than 2×3.)
The first question I’d ask you is roughly how long you needed to solve the whole set of statements and discover the unique solution. Did you see everything straight away? Five minutes? Ten? Were there any blind alleys, and fresh starts?
Secondly, you’ll want to reflect on the mathematical and reasoning skills you needed to call upon.
Thirdly, who might you see as suitable pupils for the problem?

For what it’s worth, I think it probably took me about 15 minutes, perhaps 20; I found four possibilities and had to explore each of them. It wasn’t we were working through it together that I realised there was a much better approach that avoided multiple possibilities and allows you to home in smoothly on the unambiguous solution.
And, as you’ve realised, “we” means the remarkable Amy and her partner Paddy; I’ve written before a couple of times (March 2017) about her unusually highly developed reasoning abilities. Now 55 years of teaching give me a pretty solid feeling that this isn’t a problem you dish out to your average 11-year-old (actually Amy was ten when we first me, but like me she’s had a birthday since then).
But I’ve had plenty of pupils who’ve been able to tackle this problem, and the biggest reason they can handle it is motivation. It’s one of many challenges they meet in Anita Straker’s “Martello Tower” adventure game, and by the time they’ve invested several weeks of effort they’re not going to let one more problem put them off.
Usually, however, I offer a clue or two, and my contribution with Amy and Paddy was much more limited. I did write out each of the statements onto card so they could sequence them as they wished and write on them to keep track, but otherwise

my contributions were restricted to comments like “What does that tell you?” and “What could you do next?” On completion I congratulated them, and Paddy said something to the effect that he didn’t know what I was making a fuss about, it had all seemed pretty easy!
This was our final session together, and eight weeks of working with them has reminded me yet again just how localised children’s abilities can be. Their performance in some other arithmetical problems was nothing like as advanced. In the adventure they need to identify a four-digit number using ‘more than’ / ‘less than’ clues and neither of them were great at that, and Amy was worse than Paddy. In Martello Tower they repeatedly need to use triangular numbers and neither of them ever really reached the stage where they could find TN16 without working from and earlier one like TN10 or TN12. My other pupils have almost invariably called upon the streamlined method long before the end of the adventure.
It’s not simply that some children are good at number and less so at spatial stuff, and vice versa. Amy and Paddy are able to operate a very high level in some number work, and much more mundanely at other activities even in related areas, and the difference in maturity can be quite dramatic.
I’m reminded that one year I was asked to lead the national evaluation of pupil performance in the Key Stage 2 national tests. One thing jumped out at me: for virtually every one of the hardest (level 5) questions something like 10% of the correct answers were given by children whose overall achievement was graded at below average level 3. And of course it was a different 10% each time; clearly there are a lot of Amys around, with a very jagged profile of skills across different areas of the curriculum.
Potentially this has huge consequences for the way we group and teach children, and I thought it was so important that we should be shouting it from the rooftops. But no-one else seemed at all interested, and rather to my relief the curriculum authority decided to keep the process in-house and never invited me to do the job again.
.
.
Mr Gibb and Long Division etc (part ii)
Mr Nick Gibb, Minister of State at the Department for Education, objects to certain methods of tackling questions because he claims they’re inefficient. He’s making it plain that he wants to see children using traditional calculation algorithms, and he’s particularly had the grid multiplication method and the chunking process for division in his sights. Now I see how more children tackle these processes than most, and all the evidence that I have points to grid multiplication and chunking having brought about something close to a revolution in children’s understanding and fluency. Throwing away these valuable gains in favour of a purely notional increase in efficiency seems to me little short of crazy.
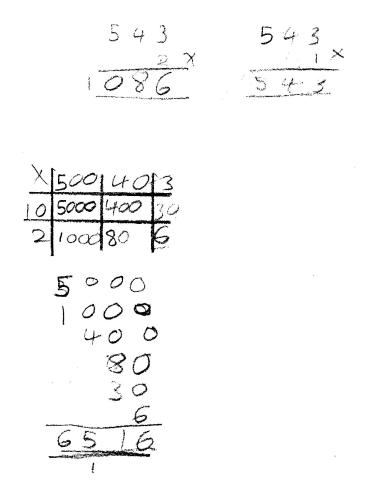
A dozen years ago I’d mark literally hundreds of children every summer who found it was the traditional long multiplication algorithm that was totally inefficient – because they couldn’t remember where or why they were supposed to be parachuting a zero or two into their operation. By contrast, the grid method allows each separate sub-product to be given the correct magnitude.
Exactly this situation occurred in yesterday’s lesson; the pupil is attempting to multiply 543 by 12. He uses the traditional algorithm and makes the classic error of multiplying first by 2 and then by 1 rather than by 10. He checked using the grid method and all the place value problems disappeared and the correct answer was reached. Which of the two methods was the inefficient one?
Today, every one of my average-attainment pupils will use the grid method with total efficiency and understanding. What’s more, unlike the standard algorithm, they use it as a basic and natural part of their toolkit to call upon when faced with new challenges. They can use the same method for every situation – three-digit by three-digit? No problem. Decimals? Lots of zeroes? And even fractions – for which the standard method is little help – they’ll use the same method for all of these. It’s not just my few pupils, either – today when I mark hundreds of pupils in their SATs papers I see the grid method used naturally and effectively as a general and reliable multiplication method.
A few weeks after Mr Gibb spoke, Freda and Joe, who were both on the level 4/5 borderline (i.e. a bit above average but by no means outstanding) got deep into triangular numbers. Effectively they were summing arithmetical progressions. They set themselves bigger and bigger challenges and surely even Mr Gibb would have been impressed how effectively they used the grid method. At one point we were walking down the corridor and Joe set himself the challenge of working out the 79th triangular number, which involved multiplying by 39½, but the grid method was so well established that he did the whole thing in his head. Go on, you have a go.
Here’s the board they filled with their calculations as the ideas and the challenges just flooded out. See how understanding the grid method is so complete that it’s become a tool that allows them to do their workings speedily without a second’s delay. All the work you see – along with more which got rubbed out – took place in a hectic burst of about 10 to 15 minutes. (One of yesterday’s pupils said “I haven’t got the time to rule a grid, I’m too busy working”.) Not much sign of inefficiency here, Mr Gibb.
With long division it’s much the same story. In this year’s Key Stage 2 Tests the long division question was 936÷36. In the conventional algorithm you first decide that you’re going to remove 720 (20 lots of 36); this leaves you with 216 which is 6 further lots of 36. This, I guess, is Mr Gibb’s preferred method – a similar calculation is done this way in a document National Curriculum Mathematics_Appendix_1 published in 2013.
Since this method involves removing first a batch of 20 lots of 36 and followed by subtracting a batch of 6 further lots of 36, someone will need to explain to me how it differs from an “inefficient” chunking method. I’m guessing – and it is only a guess – that it’s deemed as efficient because just two chunkings are used and the first of these is a multiple of 10.
I asked the statisticians for the information about the 600 000 responses to the 936÷36 question and they told me that 96% of pupils attempted the question, and 53% got the correct answer (another 9% used a valid method but made an error). These are figures that are far, far higher than anything we’ve ever seen before, and it was the chunking technique that gave children the confidence and the ability to handle the question. I can claim something like expert knowledge here, because this summer I marked no fewer than 3000 of those responses to this very question – which is a little more than 1 in every 200 children in the age-group.
Rather than a weakness, it seems a great strength of the chunking technique that you can do your chunkings however feels right to you – for example, I marked several cases where there were three chunkings, of 10, 10, and 6 lots of 36. Perhaps Mr Gibb believes using three chunkings is inefficient, though it doesn’t seem to me to devalue the method. By the way, many pupils preferred to chunk up to 936 and not down to 0. Again, that option seems a strength rather than a weakness.
Whoever is going to have to write the rules that define an approved method deserves some sympathy. When you’ve got 600 000 pupils tackling a question not everyone wants to use anything resembling the standard algorithm in the first place. For example, it’s easy to see that 936 is divisible by both 9 and by 4, so what about the children who chose to tackle division by 36 as a two-stage short-division process, dividing by 9 and then by 4? Or dividing by 6 twice? They’re not using Mr Gibb’s method, so are they being inefficient – or are they being insightful and creative?
And the response I found most memorable was the child who first subtracted 36 from 936 to leave 900, and then called upon their recognition that 900 is 25×36, so immediately getting the answer of 1+25, or 26. It’s hard to see anyone could be more insightful or efficient than that. But wait a minute, hasn’t the child has actually done a chunking, which Mr Gibb says is inefficient? Even worse, they’ve taken the smallest chunk off first, which seems to be against Mr Gibb’s procedure.
And of the 600 000 children in the cohort, some will be seriously clever and will work the question out mentally. When you can work out 936÷36 in your head, how can anyone possibly have the nerve to criticise you for being inefficient because you didn’t use a standard method?
None of this is intended as a criticism of traditional algorithms. If teachers and children see them as their preferred choice and can use them effectively and with the fluency and understanding that the National Curriculum requires, then that’s fine with me. But my observations about the grid method and chunking don’t point that way. We subject well over half a million 11-year-olds to the Key Stage 2 Tests each year, and we use the results to grade children and their schools. I’d be far more comfortable if we used the huge mass of data to tell us about the mathematics children can do and the methods they use.
.
.
Down By The Riverside – Long Division and Mr Gibb’s Laundry (part i)
I’ve heard it said that Nick Gibb does some long division practice every day before breakfast. That may or may not be true, but it may be more relevant than you think, because Mr Gibb is Minister of State at the Department for Education and it’s certainly in keeping with many of his views. Politicians do seem to attach almost mystical importance to long division, though perhaps it’s rather like doing the laundry. Everyone knows the traditional way is to go down to the riverbank and bash your washing with a rock, but I bet it’s a long time since Mr Gibb attacked his shirts with a large stone.
It might be rather nice if Mr Gibb and those in his circle – and the Education Secretary Ms Nicky Morgan certainly seems to be one of them – could be persuaded that there might be other ways of tackling mathematics in the 21st century than automatically applying a mechanical procedure. After all, I’m at the end of a very long line of people who’ve pointed out that if you want a mechanical procedure it makes a lot more sense to get a machine to do it.
I’d guess one reason Mr Gibb enjoys long division is because division feels different from the other operations. In addition, subtraction, and multiplication you have your two numbers, you do things with them (conventionally beginning with the digits of least value) and out pops the answer.
With all but the simplest divisions it works differently. You do something (starting this time with the digits of greatest value rather than the least) to find part of the answer; then you do another something and find the next part of the answer, and so on. And since finding each of these numbers may involve trying one value, and then another and perhaps another, it’s all akin to a trial and improvement process and yes, it does feel a different kettle of fish entirely.
There’s a parallel to another process. In the sixth form I learned an algorithm that was reminiscent of a long division algorithm on steroids. You thought of a number, did several things with it, did it all several times more, and eventually you found the square root (or more likely, an approximation of the square root) of the number you started with. This process was even more arcane than long division – I recall very little apart from the fact that at one point you needed to double the number you first thought of. In fact, and I may be unique here, I actually used the even more complicated procedure to find cube roots (though I’d certainly appreciate it if you didn’t ask me for any details).
Even in 1958 this was the most pointless activity you can imagine. At no time in my life did I ever need to employ these algorithms and they’ve long since passed into history. Fortunately politicians have never heard of them, so I’ve never heard even the most diehard traditionalist demand that extracting square roots ought to be a fundamental part of the mathematics curriculum. Otherwise they might still be asking students to find square roots by hand, and indeed do so in the examination room.
Don’t get me wrong; I do actually have some sneaking regard for Mr Gibb, Ms Morgan, and others in their profession. They have qualities which I totally lack, they’ve got to the top of a hugely competitive profession, they’re prepared to tackle big problems, and I don’t doubt they’re motivated by a desire to make things better. But I do wonder how Mr Gibb’s advisers (or indeed the audience) could allow him to speak dismissively of “… inefficient methods such as the grid method for multiplication and chunking for long division …” (London Thames Maths Hub Primary Conference, 27th March).
Now I’m prepared to assume we’re going to devote some curriculum time to the processes of long multiplication and long division and I want to write about these “inefficient methods” in part (ii).
.
.
Farewell, August
August is traditionally the silly season for newspapers, and there are a couple of educational stories they regularly treat us to. Firstly, there’s the grand announcement of the results, which gives columnists the perfect win-win situation. If the number of successful students goes down, then clearly educational standards are falling. And when the numbers go up – well, it’s obvious the exams are easier and hence standards must be falling.
It’s not just the writers who get busy; the photographers have an even better time. It’s truly remarkable just how many successful students are amazingly attractive young women. Judging by the photographs, only about 1% of successful candidates are boys or less attractive females.
There’s another regular August story, and this one’s more complicated and more serious as well. Each year the boundary points at which levels are awarded are liable to change slightly. So a mark of 75 may receive a different level this year to what was awarded last year. This can cause immense pain to teachers and pupils, and is liable to be interpreted by columnists as political manipulation, and by teachers as “arbitrary” or “capricious”. Now at the Key Stage 2 / 11-year-old level this is an area I know something about, and I presume the same principles apply elsewhere.
The basic factor is that it’s relatively easy to set examinations that test the syllabus or programme of study in a valid way. However, it’s quite impossible to set two examinations on the same syllabus on which pupils will perform identically, and here’s why. We’ll simplify our syllabus so that it consists of one element only, that children must master their multiplication facts; so that on a certain date in May every child will be tested and to make it fair they’ll all be tested on the same statement. Let’s say we ask them 6×9. Their papers are sent off for marking, the results are analysed, and in August the results become available and perhaps 85% of children are found to have been successful.
But what do you do next May? You could ask next year’s pupils 6×9 again, and perhaps 93% of children are successful. But in the meantime you know parents have been practising their children on 6×9, publishers have been bringing out 6×9 games, worksheets, and practice cards; schools have been putting on 6×9 practice sessions, and a thousand Youtube channels show 6×9 rhymes and raps.
So next May you decide to ask 7×8 instead, and this time 87% pass. But we don’t have much idea why this is. Is it because all the extra practice has meant children know their tables better this year? Teachers will claim the higher pass rate is down to their skill and commitment, while the government will claim a triumph for their enlightened policies. But perhaps the whole cohort is of slightly different ability. And it’s certainly true that 7×8 won’t present exactly the same level of difficulty as 6×9 to every child – some may find it easier to remember, and others harder.
And of course in the real exam there’s not just one, but dozens of questions sampling dozens of syllabus skills, so while we can be pretty sure we’re setting an exam that is fair and valid we really can’t say that a mark of 60% indicates the same level of performance as it did last year.
So just how do we ensure that a grade from last year is comparable to the same grade this year? This is vitally important and it’s a hugely sensitive issue. It’s also fiendishly difficult, and the boards use every method they can think of; many aren’t particularly watertight in themselves, but they do offer pointers. There may be an Anchor test, taken by a random selection of the age-group; the Anchor test stays the same year after year, so that gives an indication how each cohort compares to the last. Another process is that some of last year’s candidates sat this year’s paper immediately before they sat their own test, so we can reason their performance on the two tests will be similar. Of course the statisticians will be at work as well. There are likely to be other processes involved I don’t know about, but one I have experienced is where a panel of the most expert authorities sit down and examine a selection of papers at this year’s borderlines and compare them with borderline papers from previous years.
All of these are partial indicators only, and they all have disadvantages, but when they’ve all been taken into account it may be necessary to take the decision that one or more of last year’s boundaries may need to be adjusted by a point or two. I’m as sceptical about politicians as you are, but I’ve been given every assurance that this judgment is made on educational grounds and nothing else whatsoever. You can at least be certain that no examination board ever adjusts boundaries without a huge amount of thought and effort, and you can be 100% sure this is never done in an “arbitrary” or “capricious” manner.
.
.
My School – and Leapfrogs
I feel a bit of a fraud sometimes, strolling into school to do my one or two sessions a week. Clearly, I’m not more than the smallest cog in the machine. However, I get the staff emails, I have the security code for the front door and the photocopier as well, and my photo’s on the board in the entrance and on my staff badge, all of which go to confirm that I am indeed officially part of the staff. I find I’ve been there for five years, which of course is longer than all the pupils and many of the teachers.
But what makes it really special for me is that it’s the same school where I was Deputy Head not far short of 40 years ago, which means that my first pupils there are now fast closing in on their 50th birthdays. Sometimes I’ll stroll through the building calling up memories – I taught there for nearly ten years in the 70s and 80s, so there are plenty of those in every corner and every classroom.
Of course, much is completely different these days, from the moment I drive into the car park and see the new buildings and lots of girls playing football. Perhaps the biggest change is the place of the computer. 35 years ago I had to raise funds to buy our first computer, which was quite likely one of only a few dozen in the whole town, but I’m afraid left most of our staff underwhelmed. Today we have a room full of computers and every child can use a variety of programs and sees nothing remarkable about it.
And to be strictly accurate, it’s not the same school; it’s been reorganised into a different school, with a new organisation and new set of governors, and is now a primary school for 7s to 11s rather than a middle school for 9s to 13s – but they still feel like much the same pupils coming from the same streets as forty years ago. I don’t think the principles guiding what I do, or many of the activities, have changed much over the years, though I was amused when I loaded up my favourite computer adventure game for the first time in a quarter of a century. Its introductory screen says “It is a warm sunny day in 1993”, so what offered children an exploration set ten years in the future has become a trip into the past – but who cares, the program still enthuses today’s children just like those of thirty years ago.
There’s one anecdote no-one will believe. I first came to Berkhamsted in 1971. It was an exciting time and I was delighted to be the first head of mathematics and science in a brand-new middle school. The County Treasurer came to a welcome party for the staff. “We are the richest county in England”, he said. “Anything you ask for you can have!” It was true. Lorries drew up, delivering photographic enlargers and equipment we hadn’t asked for, and woodworking machines that no-one on the staff knew how to use.
Counties, and their advisory staff – and I was later lucky enough to lead the Hertfordshire advisory team for primary maths – were major sources of curriculum development on a scale that’s already just a fading memory. In-service courses, residential centres, and advisory teams all developed innovation and advice. And it wasn’t just the counties, either. The professional associations of the Mathematical Association and the Association of Teachers of Mathematics had a profile that ensured that governments willingly sought their views.
But you’ll be wondering what on earth Leapfrogs have to do with this post. It was during my first period at the school in the late 1970s that I first met some of those at the cutting edge of innovation in mathematics teaching. I joined an ATM spinoff called Leapfrogs and for three years we went to their summer conference. I say “we” because a Leapfrogs summer conference was a combination of workshop, blue-sky thinking, and family holiday for the three of us – at £10 the only one we could afford at the time.
Leapfrogs weeks were probably the most exciting development sessions of my life. Teachers, partners, young children were all involved in informal and exciting sessions which were important enough to attract university lecturers and participants from Europe and the USA. Somebody must have secured some significant funding, because several booklets which were the very antithesis of textbooks were published – you can find the Leapfrogs Link and Action books at http://www.nationalstemcentre.org.uk/elibrary/search?term=leapfrogs&order=score
I remember talking a lot of nonsense at Leapfrogs sessions, but it was an atmosphere where you could say anything and have your opinions respected, and it was a wonderful opportunity for a classroom teacher to mingle with experts and innovators from around the world.
(That’s Jill and myself at the base of the steps, vintage 1977. I can’t recall the woman at the top of the steps, and I’ve no idea who actually took the photograph.)
.
.
A Productive Conversation With Susie
I was helping out in the class of a friend, and she asked me to have a word with Susie, sitting at the back of the class. It’s a long time ago now, and I can’t begin to recall what the problem was, but I do know our conversation went pretty much like this:
.
Susie: Can you help me please? I can’t do this one.
Alan: Let’s have a look at it. What’s the problem?
S: I can’t do any of it.
A: OK. Well, how do you think you might start?
S: (Pause, then) Well, I suppose I could ….
A: That seems a good idea.
S: But what do I do next?
A: What do you think you could try?
S: (Pause, then) Well, I might do ….
A: OK
S: But what then?
A: Well –
S (Pause, then huge, radiant, smile): Oh, I see! It’s OK! I’ve got it now! Thank you so much!
.
Now I’d no wish to destroy Susie’s conviction that I’m the greatest maths teacher that ever lived, but I’d not said one insightful word about the problem. I’d not even needed to look at it – all I’d needed to do was lend an ear and a little encouragement. Any teacher, or any parent, could have done the same.
And the message? Well, an obvious one is that Susie got far more satisfaction from solving the problem herself than if I’d said “First you do this, then you do that, …”. But the bigger one for teachers and pupils is that seeing maths as a subject that has to be done at a hundred miles an hour does nobody any favours. The biggest factor in Susie’s success was being able to think her own way through the question without pressure and in her own time.
……………………………………………………………
It was Denise Gaskins in her blog Let’s Play Math ( http://letsplaymath.net/about/ ) who reminded me about Susie. Denise posted a famous clip of a couple of primary pupils tackling a problem about fractions, and if you’ve got 6½ minutes to spare you can see the video at https://www.youtube.com/watch?v=Q-yichde66s
It’s a very similar message – that by giving the girl and boy the time to tackle the problem (and the resources to do so practically) followed by the opportunity to talk about it at their own pace you get a depth of learning that goes far beyond giving them a batch of mechanical rules.
Here’s what Denise had to say: http://letsplaymath.net/2014/08/13/fractions-15-110-180-1/
.
The Best Question I Ever Asked
I was inspecting a Y3 class and came across a boy who’d been given a worksheet of fifty questions. Fifty! To my mind, if the child has mastered the skill then you don’t need anywhere like fifty examples to prove it. And if they haven’t, then it’s pretty disgraceful to give them fifty opportunities to ram their failure home more and more heavily.
When I came across Cunningham he’d reached number 34. Question 34 asked him to perform 5 – 2 . (What on earth, you may wonder, were questions 1 to 33 like?)
I couldn’t bring myself to ask him for the answer – but I did ask if he thought he could manage the challenge. Not surprisingly he felt it was within his capabilities, so I asked “Can you give me another sum which would have the same answer?”
And – instantly – he wrote 1000 – 997
It’s hard to imagine ever meeting such a horrible mismatch between what a child was capable of and what he was actually being asked to do. I didn’t much enjoy doing inspections, but this was certainly a light-bulb moment and a tribute to the power of asking open rather than closed questions.
.
.
Heroes – Peter Reynolds
Peter Reynolds played quite a rôle in my career. He invited me to join the Mathematical Association’s Diploma Board, he gave me my first speaking engagement outside my own county, and he was the first to suggest I might have something to offer schools in general rather than just my own. One day a letter arrived: “Dear Alan – have you ever thought of becoming an advisory teacher? I think you’d be excellent in that rôle. Come along for interview ….”
(I turned up, clutching my hand-written letter – and found seven others all with their individual letters! So in fact I never got to work in Peter’s team, but it was this experience that started me thinking and a couple of years later I did make the AT step in my own authority.)
Peter never sought a high profile, but he contributed enormously to mathematical education. Much of his work was done for the Mathematical Association ( http://www.m-a.org.uk ); he was the first editor of Mathematics In School, and the Diploma Board was a leading influence in the development of maths teachers. He also served on the Cockcroft committee which resulted in the hugely influential report “Mathematics Counts”.
I suspect that his image was responsible for much of Peter’s effectiveness. He was always well turned-out, and quietly well-spoken. He looked in fact like the typical grammar school teacher of my own schooldays, and was comfortable with officials and committee members. They looked at Peter and saw someone they could work with and who wouldn’t rock the boat. What they didn’t realise until it was too late is just how deceptive that image was.
Peter was in fact a deeply subversive individual and it was his influence that saw Suffolk as a hot-bed of curriculum development in mathematics. He assembled a team (sadly not including myself) of iconoclasts. Not all of them shared his impeccable dress sense, but they were all committed to innovation, most particularly in the contribution the electronic calculator could play in the development of children’s understanding on numbers. Peter’s team played a large part in Hilary Shuard’s pioneering CAN Project that we in nearby Hertfordshire followed with interest.
Peter was another who died much too early, in 2000 aged 68. Not long before, we’d worked together again on an MA group, and on the last occasion we found we were both planning to look in at Mole Jazz. Mole Jazz was at Kings Cross and even in that somewhat dilapidated area was a bit of an eyesore. I bet not one of those committee members who imagined Peter was one of themselves had ever heard of it.
.
.
It’s Official: England’s Performance Is Among The Best In The World
That’s a headline you didn’t read this week, which is a great shame, not least because it’s actually true.
Given their normal degree of accuracy and fairness I suppose it’s no surprise to see newspaper headlines like “Britain’s Stagnating Schools”, and “Anxious UK Pupils Lag Behind In Maths”. Most of our newspapers don’t need much excuse to beat up teachers, and they used the PISA reports to blast away at everything in sight.
No-one seemed to try very hard to make it clear that the information wasn’t gleaned across the whole school system, but related to tests given to 15-yearolds. Now in actual fact, pupils in primary schools in England really score rather highly in tests, regularly featuring in the top ten or better. I’ll say that again, in case any reporters are listening – primary pupil performance in England is “Very good”. I know that, because those are the words Stefano Pozzi – who’s the senior official at the DfE most responsible for leading the development of the new National Curriculum – used when he talked to a dozen of us earlier this year. The official NFER report states that “England’s performance at year 5 is amongst the best in the world and continues to improve”.
One of the countries we’re often enjoined to imitate is South Korea. There are lots of reasons why the Pacific Rim countries have such success rates, but I’m pretty certain one of the biggest is the culture that means that a quite astonishing 1.7% of the national GDP is spent on out-of-school additional tuition. That’s a cost equivalent to 80% of the total government expenditure on primary and secondary education. I suppose that as a One-To-One tutor I’m programmed to be particularly interested in this, but nearly three-quarters of South Korean children receive an average of seven hours a week of extra tuition; the government has recently been forced to pass a law that requires tutoring institutions to close by 10pm – otherwise students might still be studying in them at 1am.
.
.