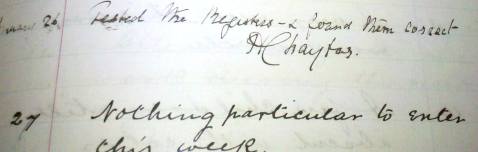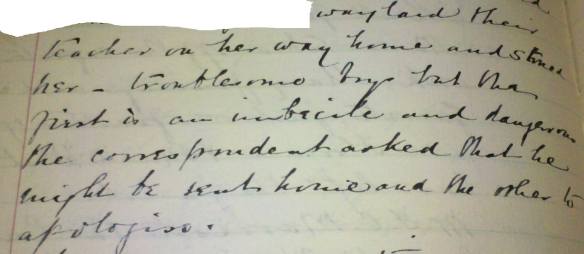“… Tables Not Well Known”
This is another posting from my history of schools findings.
For more than 150 years there’s been one yardstick that’s been used to give a quick judgment by all and sundry about mathematics learning – “Do they know their tables?” And you’ve only got to look at school logbooks or HMI reports to realise that in spite of 150 years of teachers’ efforts the answer has invariably been “No”.
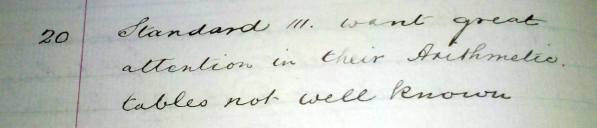
.
Long after many countries had universal elementary education England was known for having perhaps the worst schools in Europe. No-one had much interest in schooling; there had been too many revolutions in Europe for the landed gentry to want the population to become educated, and parents and employers were keen to have children – even those as young as six or seven – working for a living.
Consequently, it wasn’t until 1832 that the Government made the first tentative grant, putting £20 000 towards the building of elementary schools. Of course, the £20 000 covered the country as a whole, but a new school might cost only £60 or so, so it was a useful start. A few years later a system allowing promising pupils to train in their schools was developed, followed by the emergence of training colleges. At last elementary education in England had taken off, and growth and momentum were rapid – I found a reference as soon as 1850 to a teachers’ magazine which encouraged teachers “to make the learning of tables interesting, instead of mere mechanical routine”.
But within a few years the Government found to its horror that the £20 000 grant had grown to nearly a million pounds every year. As governments invariably do in such cases, it set up a committee, and in 1862 the draconian Revised Code was introduced. The Code soon became known as Payment By Results, for schools would only receive a grant for those children who met nationally decreed standards of attainment and attendance.
Anyone who’s been involved in education in recent times will have little difficulty in believing what happened next. Children were tested annually the “Three Rs”, Reading, Writing, and Arithmetic. Children worked in one of six levels of attainment, known as Standards. Not surprisingly, the examination became the focal point of the school year. The Head’s job security depended upon the results, so the curriculum narrowed down to the three Rs and little else, with children spending the preceding weeks or even months doing nothing but practise for the examination. I found that one school even postponed the Christmas and New Year holidays until after the Inspector’s visit!
In the run-up to the tests even Scripture lessons might be abandoned, a serious matter given how important the church, and in particular the Rector, was to most schools. For example, a week before the inspection in 1865 one Head recorded in her logbook “Instead of having Scripture Lessons children questioned on the Multiplication Table”.
The examination was carried out via a visit from one of Her Majesty’s Inspectors. Most HMI were appointed for their Church connections, usually with a university background; they’d see themselves having considerably higher social standing than a mere teacher and often they might have little understanding of children. So both teacher and children might dread the annual visit; at least one Head was so terrified by a coming inspection that she drowned herself.
The actual arithmetic syllabus could hardly have been more narrow. In Standard I, for the youngest children, the requirement was “Form on blackboard or slate, from dictation, figures up to 20. Name at sight figures up to 20. Add and subtract figures up to 10, orally, from examples on blackboard”.
Standard II required “A sum in simple addition or subtraction and the multiplication table”, and Standard III “A sum in any simple rule as far as short division (inclusive)”. For most, schooling would finish well before they reached higher Standards.
School logbooks make it clear that such a limited syllabus and so much at stake meant teachers gave the highest priority to the learning of tables. We see teachers devising the same techniques we use today – “Find the plan of getting St II to learn their Multiplication Tables at home answers well.” And “Encouraged children to get table books of their own, bring them to school and say tables from them.” Those who like to use rock or rap versions of tables are following the example of the Devon teacher of 150 years ago who encouraged her children to sing their tables from 2.30 to 3pm.
Teachers recognised the benefits of a little and often approach: “Find the II St know much of their Multiplication Table, as I devote a short time on Tuesdays and Fridays to hearing it having been learnt at home”. They seized every opportunity for a little practice, even when lining up: “Examined the children in the Multiplication Table while at the line”. I even found a Head who devised the Buddy approach used in my own school, observing, as we too find, its value to both parties: “On Thursday adopted a fresh plan for teaching Arithmetic. For about twenty minutes gave everyone on the three upper classes a child from the lower classes to teach …. Found it beneficial to both the elder and the younger ones.”
It’s frequently asserted that children used to know their tables perfectly, but it’s clear that this common belief simply isn’t true. Virtually every logbook finds Heads bemoaning their pupils’ inadequate knowledge. One Head writes in three successive months he finds it necessary to keep one class in for not learning their tables. Next year’s equivalent class is just as unsuccessful, and the year after that he finds himself keeping them behind not occasionally but every day for a week. (Declining standards, no doubt!) And this is no ogre, but a Head who joins the children at play, and enjoys snowball fights and playing cricket with them. Children bring him flowers, and worry when he’s ill. He’s constantly looking to find better ways to teach; he’s ambivalent about using the cane, but is forced to admit that other punishments don’t always work – “Find that threatening children with an extra ½ hr at school is no punishment for some say they would like staying.”
It was the Payment By Results code that required schools to keep a logbook, so logbooks aren’t actually all that rare. Some have been transcribed and others put onto CD ROM, so they can be both convenient and inexpensive to study. Much of what you read comes across as truly historical – children unable to attend because they have no boots, or absenting themselves at harvest time because they’re working in the fields. There are enormous class sizes – in one case 104 children in a room so small they had to take turns to sit down. Illness and epidemics are frequent and pupil funerals are tragically by no means unusual – one terrible story featured a family who lost each of their five children in a measles outbreak.
In other ways you find yourself thinking that things haven’t changed a bit – demanding pupils “Oliver G cannot be left a minute without his getting into mischief …”, daunting workloads and endless paperwork, publishers offering workcards and schemes promising to meet syllabus requirements, and – of course – the never-ending struggle to master the multiplication tables.
.
.
The Logbook revisited
I first published this piece two years ago following a chance encounter with a school logbook. By the end of the week the owners of the logbook had invited me to talk to their history group about the history of mathematics teaching in elementary schools. Only after agreeing did it sink in that I actually didn’t know very much at all about the subject, and I’ve spent the last couple of years trying to find out.
It’s become a major interest; I’ve explored texts, archives, reports, lots more logbooks; I’ve picked the brains of everyone I can think of and I seem to have run out of people who know more than I do. I’ve found out a lot of interesting things along the way, so I plan to make regular postings on the topic. To start the ball rolling, this is my original piece.

I spent a quite fascinating afternoon looking at an old school logbook. It used to be mandatory for schools to keep a record of events, and that the Headteacher had to make an entry at least once a week. Judging by this particular logbook, the Head would have a lot of discretion about how this requirement would be met.

Over a period of thirty years or so the job changed hands a few times, and some incumbents wrote just a single line – sometimes simply “Nothing important happened this week”.
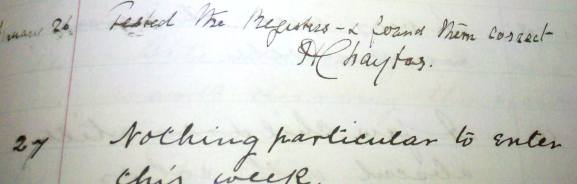
Later Heads wrote more, and as the book filled up over the years they would regularly be writing a page or more.
The school was in a village near Banbury, around halfway between London to Birmingham, and the book covers the period from the mid-1880s to 1906. Typically, roll numbers were around 75 with an infants class and another class for older children.
It was a rural community and children were often away from school helping with duties like potato-picking and harvesting, and other duties I’ve never heard of – “leasing”, and “birdminding”. The authorities were clearly pretty strict about attendance, with visits from the attendance officer and the attendance registers being audited frequently. Later Heads would state the percentage attendance for both classes every week, but clearly had the authority to use some discretion, and on one occasion decided not to open school on the day Barnum and Bailey’s circus came to town.
It wasn’t just the attendance officer that the Head had to worry about. He himself visited the classes to check on progress; the Rector visited regularly, and the Government Inspector came as well, perhaps once a year. I was a little surprised to note that often the reports of the Head and the Inspector would often give mathematics (more precisely, arithmetic) a low profile, being subsumed within “Basic” studies. Greater priority might be given, particularly in the Infants, to Handwriting, Singing, Needlework, or Recitation.

We’re told ad nauseam that in the olden days every child knew their multiplication tables. It’s not true!
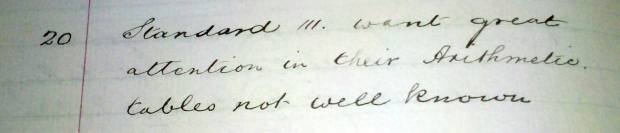
(“Standard III want great attention in their arithmetic tables not well known.”)
There’s another widespread belief – that children in the past were impeccably behaved, and that today’s society, and teachers in particular, have allowed standards of behaviour to plummet. The 1890s Head wouldn’t have seen his pupils as being impeccable. In a school of just 75 or so, half a dozen pupils are named week after week and several others less frequently. Not all of them were boys – Minnie W seems to have been a real problem, being excluded from class time after time. Her brother? / cousin? Reginald is pretty well as bad, while Oliver G “Can’t be left for a moment without getting into mischief”. One senses a grim smirk on the next page when Oliver falls off a prohibited wall and breaks his leg – but a year later he “is just as bad as before he broke his leg”.
John J was another regular offender, with a particular habit of “molesting the girls on their way to school”.
One incident shocked me when I read of the attack by Ernest L and Clement W (another relation to Minnie and Reginald!) who stoned their teacher on her way home. I’ve never heard of such an incident, and I hope the teacher was satisfied that sending offenders home and making them apologise dealt adequately with the matter.
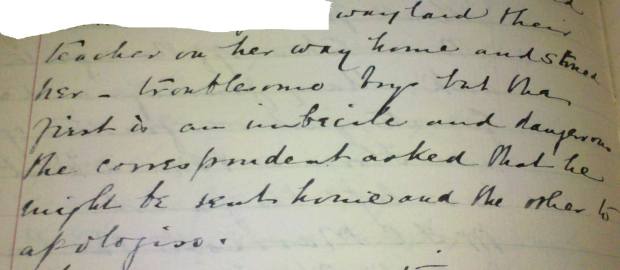
Indeed, and contrary to what one might have expected, in this school at least corporal punishment seems to have been rare. In 300 pages I found only one direct mention, when John J “an excessively bad boy … at last had a stripe this Friday afternoon”.
No doubt the teachers breathed sighs of relief when Oliver and John and Reginald left school for the last time, probably at the age of 13. Little did anyone know that several of those happy, carefree, mischievous boys had fewer than fifteen years left to look forward to. This tiny village of just a few hundred sent 86 men to fight in the Great War, and no fewer than 25 never returned. Reginald and Clement died on the Somme within a few months of each other; to the unimaginable grief of their parents both lost an elder brother as well.
.
.
The Logbook
I first published this piece two years ago following a chance encounter with a school logbook. By the end of the week the owners of the logbook had invited me to talk to their history group about the history of mathematics teaching in elementary schools. Only after agreeing did it sink in that I actually didn’t know very much at all about the subject, and I’ve spent the last couple of years trying to find out.
It’s become a major interest; I’ve explored texts, archives, reports, lots more logbooks; I’ve picked the brains of everyone I can think of and I seem to have run out of people who know more than I do. I’ve found out a lot of interesting things along the way, so I plan to make regular postings on the topic. To start the ball rolling, this is my original piece.
Recently I spent a quite fascinating afternoon looking at an old school logbook. It wasn’t until the 1870 Education Act that education became universal, and it used to be mandatory for schools to keep a record of events. The Headteacher would make an entry at least once a week; judging by this particular logbook, dating from the latter years of the nineteenth century, the Head would have a lot of discretion about how this requirement would be met.
Over a period of thirty years or so the job changed hands a few times, and some incumbents wrote just a single line – sometimes simply “Nothing important happened this week”.
Later Heads wrote more, and as the book filled up over the years they would regularly be writing a page or more.
The school was in a village with a population of 500 or so near Banbury, around halfway between London and Birmingham, and the book covers the period from the mid-1880s to 1906. Typically, roll numbers were around 75 with an infants class and another class for older children.
It was a rural community and children were often away from school helping with duties like potato-picking and harvesting, and others I’ve never heard of – “leasing”, and “birdminding”. A consequence of the 1870 Act was that the authorities were pretty strict about attendance, with visits from the attendance officer and the attendance registers being audited frequently. Later Heads would state the percentage attendance for both classes every week, but even so clearly had the authority to use some discretion (on one occasion the Head decided not to open school on the day Barnum and Bailey’s circus came to town).
It wasn’t just the attendance officer that the Head had to worry about. He himself taught fulltime and needed to supervise other classes to check on progress; the Rector visited regularly, and the Government Inspector came as well, perhaps once a year. I was a little surprised to note that often the reports of the Head and the Inspector would often give mathematics (more precisely, arithmetic) a low profile, being subsumed within “Basic” studies. Greater priority might be given, particularly in the Infants, to Handwriting, Singing, Needlework, or Recitation.
(“…. The knowledge of the elementary subjects is good on the whole, but Arithmetic is weak in the fifth and seventh standards. Geography is good, History fair, and Needlework is well done.”
Ever since I began teaching we’ve been told that in the olden days every child knew their multiplication tables. It’s not true!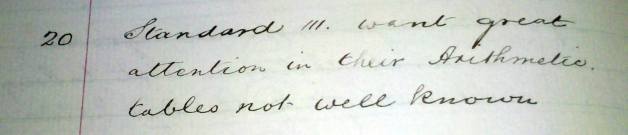
(“Standard III want great attention in their arithmetic tables not well known.”)
There’s another widespread belief – that children in the past were impeccably behaved, and that today’s society, and teachers in particular, have allowed standards of behaviour to plummet. The 1890s Head had plenty of non-impeccable pupils. In a school of just 75 or so, half a dozen are named week after week and several others less frequently. Not all of them were boys – Minnie W seems to have been a real problem, being excluded from class time after time. Her brother? / cousin? Reginald is pretty well as bad, while Oliver G “can’t be left for a moment without getting into mischief”. One senses a grim smirk on the next page when Oliver falls off a prohibited wall and breaks his leg – but a year later he “is just as bad as before he broke his leg”.
John J was another regular offender, with a particular habit of “molesting the girls on their way to school”.
I was shocked by one incident, when I read that Ernest L and Clement W (another relation to Minnie and Reginald!) attacked their teacher on her way home. I’ve never heard of such an incident, and I hope the teacher was satisfied that sending offenders home and making them apologise dealt adequately with the matter.
(“Two boys, Ernest L and Clement W, waylaid their teacher on her way home and stoned her – troublesome boys but the first is an imbecile and dangerous. The correspondent asked that he might be sent home and the other to apologise.”)
Indeed, and contrary to what one might have expected, corporal punishment seems to have been rare. In 300 pages I found only one direct mention, when John J “an excessively bad boy … at last had a stripe this Friday afternoon”. From another source I find that boys in their early teens would routinely receive fierce punishment (birching, or hard labour) for stealing items worth just a few pence, so if physical punishment at the school was indeed as rare as it seems then that does indeed surprise me.
No doubt the teachers breathed sighs of relief when Oliver and John and Reginald left school for the last time, probably at the age of 13. Little did anyone know that several of those happy, carefree, mischievous boys had fewer than fifteen years left to look forward to. This tiny village of just a few hundred sent 86 men to fight in the Great War, and no fewer than 25 never returned. Reginald and Clement died on the Somme within a few months of each other; to the unimaginable grief of their parents both lost an elder brother as well.
.
The Orchestra and The Farmyard
I used to do courses for classroom assistants who didn’t have a maths qualification. We’d do a short course at the start of September. Most had spent their lives failing in mathematics lessons, and the night before the course started some wouldn’t sleep for worry – they’d cheerfully have spent the morning with their dentist rather than with me. But when St Peter asks me why he should let me into Heaven, I’ll tell him that there are a few hundred people in the world who by the end of the course were crying with laughter that they’d enjoyed themselves so much with activities like The Orchestra and The Farmyard.
.
The Orchestra is quite simply the most fun you can ever have with a group in a maths lesson. Use it with a small group (fun), a whole class (terrific) or the entire school (brilliant).
.
Appoint about a quarter of your group to be the 2s. Their job is that whenever you count a multiple of 2 they have to stand up and sit straight down again.
So they have to go:
1 – 2 (stand / sit) – 3 – 4 (stand / sit) – 5 – 6 (stand / sit) – 7 – 8 (stand / sit) – ….
.
Another section are the 3s. Their rôle is:
1 – 2 – 3 (stand / sit) – 4 – 5 – 6 (stand / sit) – 7 – 8 – 9 (stand / sit) – 10 – ….
.
And the 4s will go:
1 – 2 – 3 – 4 (stand / sit) – 5 – 6 – 7 – 8 (stand / sit) – 9 – 10 – 11 – 12 (stand / sit) – ….
.
The final group has the easy job, so you can reserve it for those with lots of energy. They’re the 1s, and they stand / sit for every number.
.
Personally, I like to allow a little time to let each section rehearse on their own, but as soon as you’re ready you can conduct the whole performance – you make the count, and all groups perform their contributions simultaneously, no doubt with great cheers on the occasions when everyone has to stand / sit at the same time.
You’ll find all sorts of ways of implement The Orchestra in your own style, but if you want a really unforgettable experience then use the Farmyard variation – so the 2s might be chickens and have to “Cluck Cluck” each time they stand / sit, and the 3s might be donkeys, who go “Ee-aw”, ….
And while it may be the most wonderful fun, The Orchestra offers much more than that. You’ll get – and indeed feel – some quite profound insights into factors, multiples, and the like.
.
Fizz-Buzz
Everyone knows Fizz-Buzz, but since I’m putting up a number of counting games I might as well include it as a reminder. It’s another counting game you can use with a group of any size.
.
I start by introducing Fizz, which requires us to say the counting words – but replace any multiple of 3 by “Fizz”.
So the count goes:
1, 2, Fizz, 4, 5, Fizz, 7, 8, Fizz, 10, ….
.
Buzz is similar, but you have to say “Buzz” whenever you reach a multiple of 5:
1, 2, 3, 4, Buzz, 6, 7, 8, 9, Buzz, 11, 12, ….
.
And obviously the next stage is to try Fizz-Buzz, which demands:
1, 2, Fizz, 4, Buzz, Fizz, 7, 8, Fizz, Buzz, 11, Fizz, 13, 14, Fizz-Buzz!, 16, 17, ….
.
There are of course a hundred variations – change the multiples, start from a different number, start from a high number and count backwards ….
.
Find The Factors – the blog of Iva Sallay
One of the blogs I follow is Find The Factors. It’s very different from this one. For a start, it’s frighteningly efficient, and appears on a daily basis – not like this one, which happens now and again when I get around to it.
Iva Sallay gives us a new puzzle every day, where you’re given a few entries in a multiplication square and have to figure out the multipliers heading the columns and rows. So clearly we’re in an area highlighting multiplication facts – in the puzzle below the 42 in the top row has to be the product of 6 and 7 – but we can’t immediately do anything with this because we don’t know if it the 42 comes from 6×7 or 7×6. And the 20 will offer more problems, since we’ll have to discover whether it comes from the product of 2 and 10, or 4 and 5; even then, we must decide on the orientation.
A Find The Factors puzzle will be full of challenges like this, and the beauty of the blog is that they’re graded from level 1 all the way to the most challenging level 6. The puzzle below is level 4:
This puzzle is number 177, and you’ll usually get some facts about the puzzle number – its factorisation, and in this case, you’re also given a magic square made up of prime numbers; the magic total is 177.
The obvious comparison is to Sudoku puzzles. I rarely do Sudoku; I usually find I get so far and then have no option other than guessing between several possibilities until I find the right one. Just occasionally I’ve had to do this with Find The Factors, but generally speaking even at level 6 I can eventually reason the whole thing out. Mind you, sometimes I have to work hard, but that’s surely the whole idea!
I’ve shown one of Iva’s 1-12 puzzles, but she also gives 1-10 puzzles as well, and you can have a week’s worth of puzzles to download in Excel format.
You can find Iva’s blog at http://findthefactors.wordpress.com
.
I do the puzzles for my own enjoyment, but my pupils would find them daunting and indeed too time-consuming. However, the basic idea is one I’m happy to challenge them with, so I may offer them a 4×4 square constructed on the same theme. Once they’d tackled one of those, we’re likely to use the interactive version on the NRICH website (http://nrich.maths.org/7382) where you can find a variety of challenges all based on the same starting point).
.
True / False Cards
I use these a lot. They’re not threatening, they’re fun, and they’re hugely informative. The set I use most often is a simple set of a couple of dozen cards, each with a
multiplication statement, e.g. 6×6=36. Some of the statements are true, but some, such as 8×8=63, are false.
I ask children to sort them into three categories, true, false, and don’t know or not sure. What’s particularly revealing is when children tell you why they put cards into the false pile. One child will say 8×3=25 can’t be true because the correct answer must be even; another will say it’s because neither number is 5.
It’s such a valuable activity that I’ve got plenty of other sets as well, with different numbers and operations.
Using Multiplication Strips
I’m guessing, but I imagine that if you’re reading this there’s a good chance that you see a multiplication square as a beautifully structured array, logical and full of intriguing patterns, some known and some waiting to be discovered. For most of the children I work with the situation is very different. For them a tables square can be an intimidating affair, rather like one of those medieval maps of a largely unexplored continent where only the outer fringes are known and the inner areas are largely unfamiliar – “Here be dragons” indeed. In the last couple of years I’ve made much less use of a multiplication square; instead I’ve very often used a set of multiplication strips – a tables square cut into ten separate strips, one for each multiplication table. The strips are much less daunting and far more accessible, and they introduce a tactile and exploratory aspect. Give a child a multiplication square and they’ll look at it – and that’s about it. Give them a set of multiplication strips and they’ll pick them up and start to do something. Perhaps they’ll put them together and reassemble the tables square:
or often they’ll start to pair them up or sort them into groups. Sometimes they’ll sort them into two groups, the odd-numbered tables, and the even-numbered. Straight away there are interesting discoveries to be made. Choose one of the even-table strips. Can you find some odd numbers on it? No, they’re all even. So what do you expect if we look at the odd-table strips? Here’s an observation that tends to come as a complete surprise – three times as many of the numbers within a tables square are even as odd, and there are no odd numbers to be found anywhere within any even table.
More often, the initial sort puts strips into doubling pairs, x3 with x6, and x5 with x10. Immediately all sorts of questions arise. If you pair x2 with x4, then what do you do with the x8, and the x1? So in fact some of your sorting puts the strips into families rather than pairs. Once you’ve got the x1, x2, x4, x8 family isn’t it tempting to wonder if there’s not a further member waiting to be included – so you can incorporate the x16, and … ? And when you sort into pairs, what about those strips which don’t have a partner, like the x7 ? Perhaps we really ought to have a x14 strip? Or could we have a x1½ strip to provide an alternative partner for the x3 ? Of course none of these questions arise every time, but all of them are questions which have arisen with my pupils, and I find it useful to have some empty strips on hand. There’s no need actually to write out the full x14 table onto the strip, simply labelling it x14 makes the point perfectly well.